第12回:データ分析入門(講義)#
担当:古居彬
内容#
第12回では,Pythonを用いた基礎的なデータ分析を体験する. 本講義の初回で述べたように,Pythonはデータ分析や機械学習,Webサービスなど幅広い分野で利用されている. その大きな理由として,さまざまな処理を実現するための機能が豊富に準備されていることが挙げられる. このような機能を管理しているのが,モジュール と呼ばれる単位である.モジュールには,さまざまな関数が含まれている. データ解析や画像処理といった高度な処理も,それぞれの用途に特化したモジュールを組み合わせることで比較的簡単に実行することができる. また,モジュールを複数集めたものを ライブラリ や パッケージ と呼ぶ. 今回は実践編として,いくつかのモジュールを用いてPythonによる簡単なデータ分析を行っていこう.
モジュール,ライブラリ,パッケージとその使い方を理解する
Pandasによるデータ操作を学ぶMatplotlibによるデータの可視化を学ぶ
Pythonにおけるモジュール,パッケージ,ライブラリ#
前述の通り,Pythonの強みの一つは,さまざまな処理を実現するための機能が準備されており,幅広い分野に応用できることである. このような機能を管理する単位は モジュール と呼ばれ,その中にはいくつかの関数やクラスが含まれている.
また,複数のモジュールをまとめたものを パッケージ と呼ぶ.
さらに,いくつかのパッケージをまとめて,一括でインストールできるようにしたものを ライブラリ と呼ぶ. ライブラリには大きく2種類があり,Pythonにはじめから付属していてすぐに使える 標準ライブラリ と,追加でインストールすることで利用可能な 外部ライブラリ がある.
以上をまとめた概念図は以下の通りである.

ざっくり「モジュールやライブラリを利用することで,データ解析や画像処理など,高度な機能が利用できるようになる」と理解してもらえれば大丈夫だ.
Pythonの標準ライブラリ#
前述の通り,標準ライブラリとはあらかじめ用意されているライブラリである. 第8回 関数とスコープ で紹介した組み込み関数も,この標準ライブラリの中に含まれている.
組み込み関数は何もせずそのまま使うことができたが,特殊な機能を持つモジュールは後述する import 文で読み込む必要がある.
Pythonの標準ライブラリで提供されている関数・モジュールの一覧は以下の公式ページから参照することができる.
Pythonの外部ライブラリ#
標準ライブラリだけでもかなり幅広い処理が実現できるが,データ分析や画像処理,統計解析や科学技術計算など,特定の分野に特化した機能を利用するためには,外部ライブラリを利用する必要がある.
外部ライブラリは,その名の通り外部の団体や個人によって開発,提供されているライブラリである.
外部ライブラリを利用するためには,まず初めにインストールが必要である.
インストールされた外部ライブラリは,後述する import 文で読み込むことができる.
なお,Google Colaboratoryでは既に主要な外部ライブラリがインストールされており,これらは最初から import 文で読み込みが可能である.
インストール済ライブラリの表示
Google Colaboratoryにインストールされているライブラリ一覧を表示したい場合は,コードセルにて以下のコマンドを実行すればよい.
!pip list
以下のように,大量のパッケージが表示されるはずだ.
Package Version
----------------------------- ----------------------
absl-py 1.3.0
aeppl 0.0.33
aesara 2.7.9
aiohttp 3.8.3
aiosignal 1.2.0
alabaster 0.7.12
albumentations 1.2.1
altair 4.2.0
appdirs 1.4.4
arviz 0.12.1
… (以下省略) …
なお,本講義で利用する外部ライブラリについても,上記インストール済リストに含まれるため,新たにインストールの手順を踏む必要はない. 外部ライブラリを自分で追加インストールする方法を学びたい人は,以下の発展項目を参照されたい.
【発展】外部ライブラリをインストールする方法
Pythonで利用可能な外部ライブラリは,Python Package Index(PyPl) というソフトウェアリポジトリで管理されている. ざっくり表現すると,外部ライブラリのカタログのようなものである.
以下のサイトより,インストール可能な外部ライブラリを検索することができる.
pip などのパッケージ管理システムを利用することで,PyPlに登録されているライブラリやパッケージをダウンロード&インストールすることができる. Google Colaboratoryにおける外部ライブラリも,このpipというシステムによって管理されている.
Google Colaboratoryで新しい外部ライブラリをインストールしたい場合,コードセルにて次のコマンドを実行すれば良い.
!pip install ライブラリ名
モジュール/ライブラリのインポート#
前述の通り,モジュールやライブラリに含まれる関数やクラスを使用するためには,対象となるモジュール/ライブラリを読み込む( インポート する)必要がある.
これには, import という文を使う.以下のように記述することでモジュールをインポートできる.
import モジュール名
または
import ライブラリ名
モジュール/ライブラリのインポートは,最初に1回記述すればよい.
試しに,数学関係の便利な関数をまとめた math というモジュールをインポートしてみよう.
import math
これで,math モジュールが使えるようになった.
math モジュールに含まれる関数を使用するためには, math.関数名 のように記述すればOKである.
例えば,平方根を計算したいときは math.sqrt() のように記述する.
math.sqrt(2)
1.4142135623730951
ほかにも math モジュールには様々な関数が用意されている.
以下に,いくつかの例を示す.
関数 |
説明 |
|---|---|
|
|
|
|
|
|
|
自然対数の底(ネイピア数)の |
|
|
|
|
そのうちいくつかを実行してみよう.
print(math.log(13)) # 自然対数
print(math.sin(math.pi/4)) # 正弦(サイン)
2.5649493574615367
0.7071067811865475
また,math モジュールには関数の他にも,数学で多用される 定数 も含まれている.
以下に代表例を表示してみる.
print(math.pi) # 円周率
print(math.e) # 自然対数の底(ネイピア数)
3.141592653589793
2.718281828459045
モジュールに別名をつける#
モジュールをインポートする際,別の名前(例えば短縮名)を付けることが可能である.
import モジュール名 as 短縮名
例えば,以下のように書くことで,モジュール math に短縮名 m を付けてインポートすることができる.
import math as m
このようにインポートすることで,math モジュールに含まれる関数を使用する際, m.関数名 のように簡潔に書けるようになる.
m.sqrt(2)
1.4142135623730951
【発展】特定の関数だけを読み込む#
モジュールやライブラリを用いる際,特定の関数だけを読み込みたいことがある. そのような場合は,以下の表記を用いて指定した関数・クラスだけをインポートすることができる.
from モジュール名 import 関数名
from でモジュール名を指定し,続く import に読み込みたい関数・クラスを指定する(複数の関数・クラスを指定したい場合は,カンマ区切りで並べて書く).
このようにしてインポートした場合,モジュール名を記述しなくとも,関数・クラスをそのまま呼び出すことができる.
from math import sqrt
sqrt(3)
1.7320508075688772
ワイルドカードを用いたインポート
なお,次のようにアスタリスク(*)を用いると,対象のモジュールに含まれるすべての関数やクラスを一気にインポートできる.
from モジュール名 import *
なお,この際の * は ワイルドカード と呼ばれ,任意の文字列を意味している.
したがって,対象のモジュール内の任意の文字列を名前として持つ関数やクラス(つまり,すべての関数やクラス)をインポートする,という表記法である.
上記のようなインポートの方法は ワイルドカードインポート とも呼ばれ,一見楽な方法に思えるが,一般的なPythonプログラミングにおいては 推奨されない ことが多い.
理由はいくつかあるが,最も多いトラブルは関数や変数の名前衝突である.
通常,外部モジュールや外部ライブラリに含まれている関数やクラス,定数を全て把握していることは少ない. ワイルドカードインポートではそれら把握できていない物も含め全てがインポートされてしまうため,自分が別で定義した関数やクラスの名前がインポートした関数やクラスの名前と衝突する危険がある.
名前の衝突が起こると,変数や関数が上書きされてしまうリスクがあるため,基本的にはワイルドカードインポートは使わない方がよいだろう.
モジュール,パッケージ,ライブラリのまとめ
複数の関数やクラスをまとめたものをモジュールと呼ぶ
モジュールをさらにまとめたものをパッケージやライブラリと呼ぶ
外部ライブラリを追加インストールすることで,様々な追加機能が使えるようにある
モジュールやライブラリは
import文で読み込むことができる
なお,これ以降は代表的な外部ライブラリである pandas と matplotlib を用いてデータ分析に取り組んでいく.
これら2つのライブラリはそれぞれ膨大な数のモジュールを含んでおり,それらの網羅的な紹介は本講義では行わず,各ライブラリの機能を体験する上で最小限の説明にとどめる.
将来的にPythonでプログラミングをする機会が生じたときに,各自で検索しながら様々な具体的な機能を学んで行って欲しい. プログラミングにおいては,網羅的な知識を有しておくよりも,必要に応じて適切に情報を検索し利用する能力の方が重要である.
Pandas によるデータ操作#
では,実際にデータ分析の本題に入っていこう. 今回は,Pandas というライブラリを用いる. Pandasは,データ解析を容易に行うための機能を提供しており,データの操作や加工,分析などさまざまな処理を行うことができる.
以下のコマンドで,まずはPandasをインポートしよう.
import pandas as pd
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
なお,簡単のため as を用いて pd という短縮名でインポートした.
Series と DataFrame#
Pandasでは,Series(シリーズ) や DataFrame(データフレーム) といった特殊なデータ構造が使用される. Seriesは1次元(列形式)のデータ,DataFrameは2次元(行列形式)のデータを扱うための構造である.
実際のデータ分析の場面では2次元のデータを扱うことが多いため,本講義では2次元のデータ構造であるDataFrameを主に扱っていく.
DataFrameは前述の通り,行と列の2次元で表現され,表のような構造となっている. それぞれの列に対して,文字列型や数値型など,一様な型のデータが格納されている.
列と行にはそれぞれ列名と行名(またはインデックス)が付けられており,これらを指定することで,データの集計や抽出,加工に利用することができる.
DataFrameからSeriesを抽出する
DataFrameから抽出した1行または1列の情報は,1次元のデータ構造であるSeriesとなる. 逆に,複数のSeriesを結合してDataFrameとして扱うこともできる.
このように,DataFrameは複数のSeriesの集合と考えることができる.
DataFrameを作成するには,以下のようなコードを書けば良い.
pd.DataFrame(data=格納するデータ, index=行名, columns=列名)
このとき,引数の data には,リスト型や辞書型の変数を指定することができる(復習 → 第2回).
本講義では,ファイルに格納された情報をDataFrameに取り込んで解析に利用していくこととする.
データの読み込み#
今回は,アイスクリーム屋さんで学ぶ楽しい統計学 というサイトで公開されている架空のデータを用いてデータ分析に取り組んでいく.
まず,当該データをダウンロードしよう.
以下のセルを実行すると,data フォルダの中に ice_cream.csv というファイルがダウンロードされる.
!mkdir data
!wget -P data https://raw.githubusercontent.com/ground-zero-programming/zero-pro2024-public/main/docs/12/data/ice_cream.csv
mkdir: data: File exists
--2025-01-08 12:46:56-- https://raw.githubusercontent.com/ground-zero-programming/zero-pro2024-public/main/docs/12/data/ice_cream.csv
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 2606:50c0:8000::154, 2606:50c0:8001::154, 2606:50c0:8002::154, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|2606:50c0:8000::154|:443...
connected.
HTTP request sent, awaiting response...
200 OK
Length: 174 [text/plain]
Saving to: 'data/ice_cream.csv.1'
ice_cream.csv.1 0%[ ] 0 --.-KB/s
ice_cream.csv.1 100%[===================>] 174 --.-KB/s in 0s
2025-01-08 12:46:56 (3.02 MB/s) - 'data/ice_cream.csv.1' saved [174/174]
本講義の範囲内では上記のコードが何をやっているかを意識する必要はないが,簡単に説明しよう.
!mkdir dataでGoogle Colab内にdataという名前がついたフォルダを作成し,以降の!wget -P data {URL}でURLにあるファイルを先ほど作成したdataフォルダにダウンロードするという操作をしている.
さて, ice_cream.csvには,あるアイスクリームチェーン店における8月の客数データ(2週間 = 14日分)が格納されている.
このファイルは CSVファイル と呼ばれ,以下のように各データの間がコンマ , で区切られている.
日付, 最高気温, 客数
1, 29, 312
2, 30, 348
3, 29, 284
...
1行目は列のタイトル(ヘッダとも呼ばれる)となっており,2行目から各日付におけるデータが格納されている. また,暑い日にはアイスクリームを食べたいと思う人が増えるかもしれない. そこで,このファイルには各日付における客数以外に,その日の最高気温も含まれている.
CSVファイルを読み込むには,Pandasに含まれる read_csv という関数が便利である.
read_csv 関数は,目的とするファイルの保存場所までの経路(これを パス といいます)を文字列として引数に渡すことで,そのファイルを開くことができる.
今回は data というフォルダに入っている ice_cream.csv を開きたいので,'data/ice_cream.csv' という文字列を渡せばOK.
ここで,スラッシュ / はパスを記述する際の区切り文字で, A/B と書くとフォルダ A の中に B があることを意味する.
# ファイルを `df` という変数に読み込む
df = pd.read_csv('data/ice_cream.csv')
# dfの中身を表示
df
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 0 | 1 | 29 | 312 |
| 1 | 2 | 30 | 348 |
| 2 | 3 | 29 | 284 |
| 3 | 4 | 32 | 369 |
| 4 | 5 | 33 | 420 |
| 5 | 6 | 32 | 536 |
| 6 | 7 | 34 | 652 |
| 7 | 8 | 27 | 275 |
| 8 | 9 | 28 | 294 |
| 9 | 10 | 32 | 368 |
| 10 | 11 | 34 | 451 |
| 11 | 12 | 32 | 405 |
| 12 | 13 | 30 | 458 |
| 13 | 14 | 28 | 422 |
上の出力の結果から,「日付」,「最高気温」,「客数」の3つの列で構成されるデータが読み込まれていることがわかる. なお,一番左の列はPandasによって付けられた行のインデックスである.このインデックスは0からスタートしていることに気をつけよう.
列名(ヘッダ)の認識
read_csv 関数では,デフォルトでCSVファイル中の1行目の情報を列名(ヘッダ)として解釈してくれる.
先ほど読み込んだ ice_cream.csv はまさに1行目にヘッダが入っていたため上手くいったが,場合によってはヘッダのないCSVファイルを読み込むこともあるだろう.
そのような場合は,read_csv 関数の引数として header=None とすればよい.
df = pd.read_csv('data/sample_no_header.csv', header=None)
また,列名を自分で設定したい場合は,引数 names で指定できる.
df = pd.read_csv('data/sample_no_header.csv', header=None, names=['A', 'B', 'C', 'D'])
列の抽出#
データフレームから任意の列を抽出したい場合,DataFrame['列名'] のように書けばよい(文字列として指定するため,クォーテーション ' で囲っていることに注意).
例えば上記 df から「最高気温」の列を取り出したい場合は,以下の通りである.
df['最高気温']
0 29
1 30
2 29
3 32
4 33
5 32
6 34
7 27
8 28
9 32
10 34
11 32
12 30
13 28
Name: 最高気温, dtype: int64
同様にして,「客数」の列を取り出してみよう.
df['客数']
0 312
1 348
2 284
3 369
4 420
5 536
6 652
7 275
8 294
9 368
10 451
11 405
12 458
13 422
Name: 客数, dtype: int64
なお,複数の列を取り出したい場合は,取り出したい列名のリスト ['列1', '列2', '列3', ...] を DataFrame[ ] の括弧 [ ] の中に記述すればよい.
DataFrame[['列1', '列2', '列3', ...] ]
括弧 [ ] が二重になっていることに注意すること.
例えば最高気温と客数の両方を取り出したい場合は,以下のような書き方になる.
df[['最高気温', '客数']]
| 最高気温 | 客数 | |
|---|---|---|
| 0 | 29 | 312 |
| 1 | 30 | 348 |
| 2 | 29 | 284 |
| 3 | 32 | 369 |
| 4 | 33 | 420 |
| 5 | 32 | 536 |
| 6 | 34 | 652 |
| 7 | 27 | 275 |
| 8 | 28 | 294 |
| 9 | 32 | 368 |
| 10 | 34 | 451 |
| 11 | 32 | 405 |
| 12 | 30 | 458 |
| 13 | 28 | 422 |
行の抽出#
コロン(:)で行のインデックスを指定することで,特定の区間の行を抽出することができる.
例えば,2行目から5行目までを抽出したい場合は,スライシングを用いて以下のように書けば良い.
df[2:5]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 2 | 3 | 29 | 284 |
| 3 | 4 | 32 | 369 |
| 4 | 5 | 33 | 420 |
【発展】 iloc を用いて特定の行・列を抽出#
iloc を利用すると,DataFrameに対して行番号と列番号を指定してデータを抽出することが可能である.
DataFrame.iloc[行番号, 列番号]
例えば1行目を抽出する場合は,以下のように書けば良い.なお,行番号のみを指定する場合,列番号の指定は省略できる.
df.iloc[1]
日付 2
最高気温 30
客数 348
Name: 1, dtype: int64
また,3行目から6行目を抽出したい場合は,スライシング(復習 → 第2回)を利用して以下のように書くことができる.
df.iloc[3:6]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 3 | 4 | 32 | 369 |
| 4 | 5 | 33 | 420 |
| 5 | 6 | 32 | 536 |
今度は列を考える.
例えば2列目を抽出したい場合は,行の指定を : (すべての行という意味)とし,列の指定を 2 とする.
df.iloc[:, 2]
0 312
1 348
2 284
3 369
4 420
5 536
6 652
7 275
8 294
9 368
10 451
11 405
12 458
13 422
Name: 客数, dtype: int64
これらを組み合わせ,例えば2列目の3行目から6行目を抽出したい場合は,以下のように書けばよい,
df.iloc[3:6, 2]
3 369
4 420
5 536
Name: 客数, dtype: int64
条件による抽出#
True または False を返す条件式を指定することで,データフレームから条件を満たす任意の行を抽出することができる.
例えば,データフレーム df から,「最高気温が30度より大きい」の行だけ抜き出したいとしよう.
これを表す条件式は, df['最高気温'] > 30 となる.
実際に実行してみよう.
df['最高気温'] > 30
0 False
1 False
2 False
3 True
4 True
5 True
6 True
7 False
8 False
9 True
10 True
11 True
12 False
13 False
Name: 最高気温, dtype: bool
縦に True と False がズラッと並んでいるが,これはデータフレーム df のうち,どの行が条件式 df['最高気温'] > 30 を満たすかを表している.
上記の出力で条件式が満たされる(つまり True になっている)のは,行インデックスが「3, 4, 5, 6, 9, 10, 11」の場合であることがわかる.
実際に上の方で出力した df の中身と照らし合わせてみよう.
True となっている行における最高気温が30度よりも大きくなっているはずだ.
最終的には, DataFrame[条件式] のように書くことで,条件式を満たす行のみを取り出すことができる.
df[df['最高気温'] > 30]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 3 | 4 | 32 | 369 |
| 4 | 5 | 33 | 420 |
| 5 | 6 | 32 | 536 |
| 6 | 7 | 34 | 652 |
| 9 | 10 | 32 | 368 |
| 10 | 11 | 34 | 451 |
| 11 | 12 | 32 | 405 |
同様に,「客数が400より少ない」行だけを抜き出してみよう.
df[df['客数'] < 400]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 0 | 1 | 29 | 312 |
| 1 | 2 | 30 | 348 |
| 2 | 3 | 29 | 284 |
| 3 | 4 | 32 | 369 |
| 7 | 8 | 27 | 275 |
| 8 | 9 | 28 | 294 |
| 9 | 10 | 32 | 368 |
このうち,さらに「客数が400より少ない」行について,「最高気温」だけを抜き出したい場合は,DataFrame[条件式]['列名'] のように,列名を指定する [ ] を後ろにくっ付ければよい.
df[df['客数'] < 400]['最高気温']
0 29
1 30
2 29
3 32
7 27
8 28
9 32
Name: 最高気温, dtype: int64
複数条件による抽出#
単一の条件ではなく,複数の条件を使って行を抽出することもできる.
そのためには,条件分岐の回で学んだ論理演算子の考え方で各条件を繋げればよい.
ただし,条件分岐の際とは以下の2点が異なる.
条件分岐のときに用いた
andとorは使えない.DataFrameに対して複数の条件を設定する際は,andの代わりに&,orの代わりに|を使う必要がある.各条件は括弧
()で囲む必要がある.
例えば,「客数が400より少ない」かつ「最高気温が30度以上」の行だけを抽出したい場合は,以下のように書く.
df[(df['客数'] < 400) & (df['最高気温'] >= 30)]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 1 | 2 | 30 | 348 |
| 3 | 4 | 32 | 369 |
| 9 | 10 | 32 | 368 |
同様に,「最高気温が30度未満」または「最高気温が33度以上」の行だけを抽出したい場合は,以下のように書く.
df[(df['最高気温'] < 30) | (df['最高気温'] >=33)]
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| 0 | 1 | 29 | 312 |
| 2 | 3 | 29 | 284 |
| 4 | 5 | 33 | 420 |
| 6 | 7 | 34 | 652 |
| 7 | 8 | 27 | 275 |
| 8 | 9 | 28 | 294 |
| 10 | 11 | 34 | 451 |
| 13 | 14 | 28 | 422 |
要約統計量の算出#
データが与えられた時,生の数字だけを見てもなかなか情報は得られない. 多くの場合,データの特徴を要約した数値を計算し,全体の傾向の掴んだり,さまざまな条件で比較したりする.
このとき計算される数値のことを 要約統計量 や 記述統計量 と呼ぶ. これには様々な種類があるが,今回は最も基本的な5つの要約統計量を計算してみよう.
各統計量は,データフレームに対して以下のように書くことで計算できる.
DataFrame.統計量()
今回はデータ中の最高気温に対して,各種統計量を計算してみる.
最小値(min):データに含まれる最も小さい数.
minimum = df['最高気温'].min() # 最小値の計算
print(minimum)
27
最大値(max):データに含まれる最も大きい数.
maximum = df['最高気温'].max() # 最大値の計算
print(maximum)
34
平均値(mean):データの中間的な値を表す統計量.\(N\) 個のデータ \(x_1, x_2, \ldots, x_N\) に対して,以下のようにデータの合計を個数で割ることで計算される.
mean_value = df['最高気温'].mean() # 平均値の計算
print(mean_value)
30.714285714285715
分散(var):データのばらつき具合を表す統計量.以下の式で計算される.
variance = df['最高気温'].var() # 分散の計算
print(variance)
5.296703296703297
標準偏差(std):分散 \(s^2\) の平方根で計算される.分散は各データを2乗した値から求めているため,平均と比較することができない.分散の平方根を計算することで,データのばらつきを平均を比較できるようになる.
stdev = df['最高気温'].std() # 標準偏差の計算
print(stdev)
2.3014567770660603
以上をまとめると,14日間における最高気温は27度から34度の範囲で変化し,平均値は約30.7度,標準偏差は約2.3度なので,値のばらつきはそこまで大きくないことがわかった.
なお,上記の例では一つ一つ記述統計量を算出したが,describe() メソッドを用いることで,DataFrameの各列に対して複数の要約統計量を一気に計算することもできる.
df.describe()
| 日付 | 最高気温 | 客数 | |
|---|---|---|---|
| count | 14.0000 | 14.000000 | 14.000000 |
| mean | 7.5000 | 30.714286 | 399.571429 |
| std | 4.1833 | 2.301457 | 104.374116 |
| min | 1.0000 | 27.000000 | 275.000000 |
| 25% | 4.2500 | 29.000000 | 321.000000 |
| 50% | 7.5000 | 31.000000 | 387.000000 |
| 75% | 10.7500 | 32.000000 | 443.750000 |
| max | 14.0000 | 34.000000 | 652.000000 |
Pandasによるデータ分析のまとめ
Pandasというライブラリを用いることで,データの収集や整理,加工が容易となる
PandasではDataFrameやSeriesといったデータ構造が利用される
DataFrameの列や行に対してに対して条件式などを用いた用いた抽出が可能である
Matplotlib によるデータの可視化#
データ分析において,集計した結果を図やグラフなどを用いて視覚的に表示してみることは非常に重要である. そのデータから読み取ることができる情報と,それに基づく意思決定にまで影響を及ぼす. このような操作を,データの 可視化(visualization) と呼ぶ.
ここでは,グラフ描画用ライブラリである Matplotlib のモジュールを使用して,データを可視化するためのグラフを作成していく.
Matplotlibライブラリを使用するためには,まず matplotlib のモジュールをインポートする.
ここでは,基本的なグラフを描画するための matplotlib.pyplot というモジュールを使用する.
慣例として,同モジュールに plt という短縮名を付けて利用しよう.
import matplotlib.pyplot as plt
%matplotlib inline
なお,%matplotlib inline は,ノートブック内でグラフを表示するために必要なコードである.
なお,以下はMatplotlibで日本語フォントを扱うための設定用コードなので,実行だけして中身は無視して構わない.
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['Hiragino Sans', 'Yu Gothic', 'Meiryo', 'Takao', 'IPAexGothic', 'IPAPGothic', 'VL PGothic', 'Noto Sans CJK JP']
【補足】上記コードが気になる人向けの解説
上記のコードについて簡単に解説する(気にならない人はスルーしてよい).
まず一行目では,Matplotlibに含まれる rcParams という辞書形式のオブジェクトをインポートしている.
ここにはさまざまなデフォルト設定値が格納されており,この設定値を変更することで,プログラム全体のグラフに対して見た目などの変更が可能である.
rcParams['font.family'] を変更することで,グラフ中のフォントを任意に設定できる.
ただし,使用しているPC環境(OSやブラウザ)によっては特定のフォントが使えたり使えなかったりするため,フォントの大きなカテゴリ(総称フォントと呼ばれる)である sans-serif を設定している.
rcParams['font.family'] = 'sans-serif'
sans-serif とは日本語フォントでいうところのゴシック体である.
また,rcParams['font.sans-serif'] を変更することで,sans-serif として利用可能なフォントの選択肢を具体的に指定している.
rcParams['font.sans-serif'] = ['Hiragino Sans', 'Yu Gothic', 'Meirio', 'Takao', 'IPAexGothic', 'IPAPGothic', 'VL PGothic', 'Noto Sans CJK JP']
このうち,使用しているPC環境が利用可能なものがグラフ中のフォントとして使用される.
例えば,Macであれば必ず Hiragino Sans が利用可能であり,Windowsであれば Yu Gothic や Meirio が,Ubuntuであれば Noto Sans CJK JP が使えるはずである.
そのため,一般的なPC環境であれば,OSやブラウザを問わず正しく日本語フォントでグラフを出力できるようになっている.
線グラフ#
pyplotモジュールに含まれている plot 関数を用いて,線グラフを描画していこう.
plt.plot(X, Y)
と書くことで,x軸に変数 X,y軸に変数 Y を取った線グラフを表示することができる.
このとき,X と Y にはリストやPandasのSeries,DataFrameなど様々指定できる.
まずは,「日付」によって「客数」がどう変わるかをグラフ化してみよう. x軸に日付,y軸に客数を指定してグラフを描画すればよい.
plt.plot(df['日付'], df['客数']);
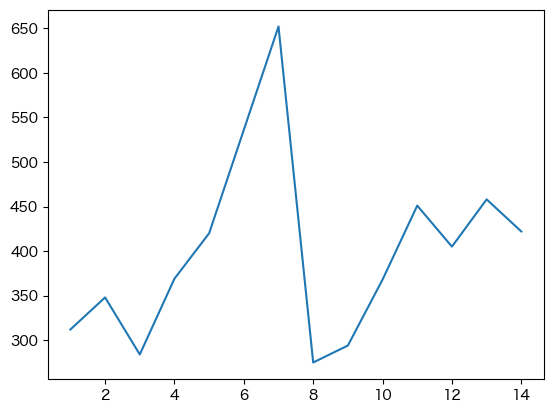
なお,セルの最後に実行されたオブジェクトの出力表示を無くすため,これ以降グラフを描画する際は,セルの最後の行にセミコロン(;)をつけていることに注意されたい(セミコロンが無くてもグラフ自体は問題なく描画できる).
plot 関数ではグラフの線の種類や色,データポイントのマーカの種類を,様々な引数で指定できる.
例えば,先ほど作成した線グラフにデータポイントの丸型マーカを加えたい場合,plot 関数の引数に marker='o' を追加する.
plt.plot(df['日付'], df['客数'], marker='o');
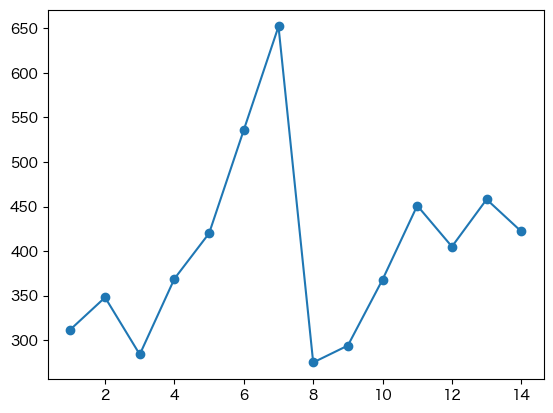
引数 marker に違う値を指定するとマーカの形状が変わる.
plt.plot(df['日付'], df['客数'], marker='x');
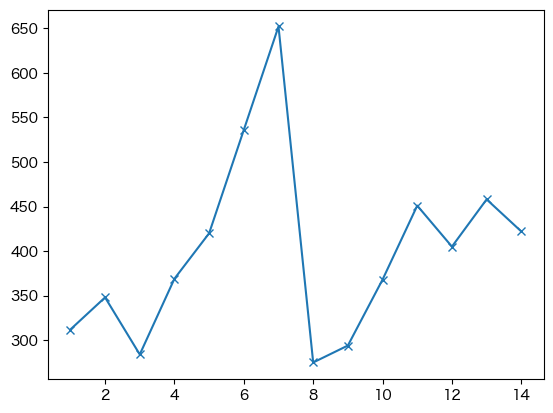
他にも,linestyle で線の種類を変えたり,color で線の色を変更したりできる.
plt.plot(df['日付'], df['客数'], marker='*', linestyle='--', color='green');
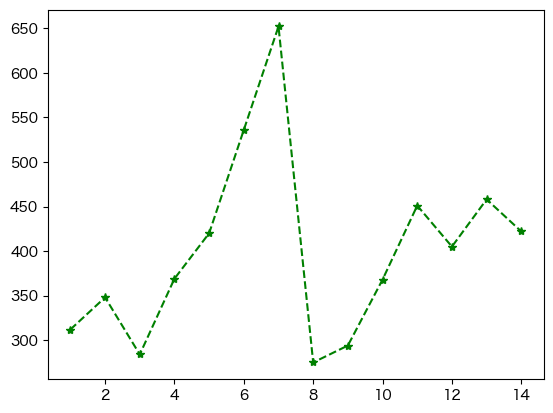
それぞれの引数で指定可能な値は以下を参照されたい.
pyplot モジュールでは,グラフのタイトルと各軸のラベルを指定して表示することができる.
タイトルは title 関数,x軸のラベルは xlabel 関数,y軸のラベルは ylabel 関数に文字列を渡すことで指定可能である.
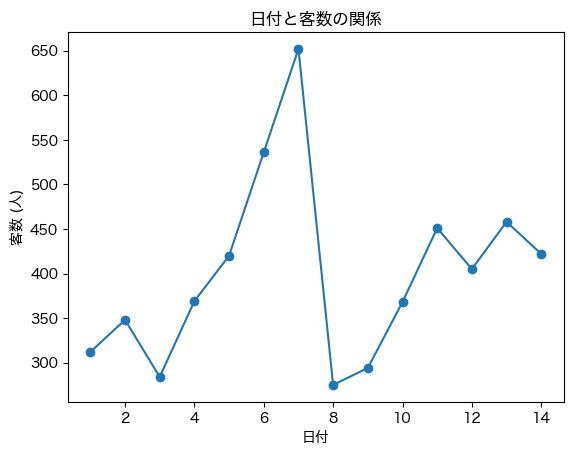
plt.plot(df['日付'], df['客数'], marker='o') # グラフを作成
plt.title('日付と客数の関係') # タイトルを追加
plt.xlabel('日付') # x軸のラベルを追加
plt.ylabel('客数 (人)'); # y軸のラベルを追加
タイトルなどが文字化けする場合
PC環境によっては,日本語フォント表示用コードを実行してもグラフ中に日本語がうまく表示されず,文字が □ のように表示されることがある.
その場合は,以下のコードをコードセルに貼り付け,実行してからグラフを描画せよ.
!pip install japanize-matplotlib
import japanize_matplotlib
japanize_matplotlib.japanize()
同様に,「日付」によって「最高気温」がどう変わるかを線グラフで描画してみよう.
plt.plot(df['日付'], df['最高気温'], marker='o') # グラフを作成
plt.title('日付と最高気温の関係') # タイトルを追加
plt.xlabel('日付') # x軸のラベルを追加
plt.ylabel('最高気温(度)'); # y軸のラベルを追加
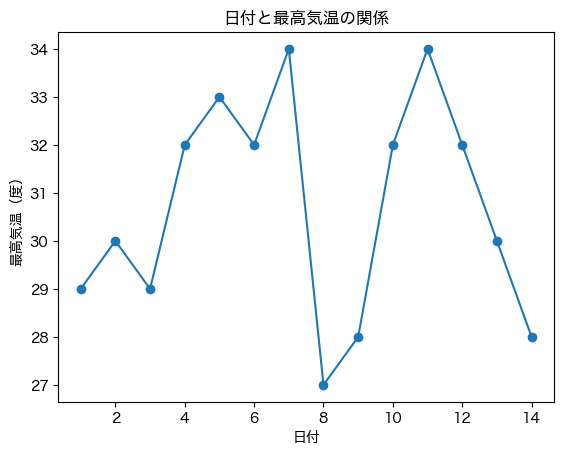
さて,では「日付と客数」のグラフと,「日付と最高気温」のグラフを交互に見てみましょう. 何か気がつくことがないだろうか?
最高気温が高い日には客数も多く,最高気温が低い日には客数が少ない傾向があるように見える.
2つの変数の関係を可視化するために,次に 散布図 というグラフで最高気温と客数の関係を見ていこう.
散布図#
散布図とは,横軸と縦軸に異なる要素を設定し,それらの関係性を調べる際に用いられる.
Matplotlibでは,pyplot モジュールの scatter 関数を用いて描画することができる.
次のように,
plt.scatter(X, Y)
と書くことで,x軸に変数 X,y軸に変数 Y を取った散布図を作成できる.
このとき,線グラフの場合と同様に,さまざまな引数を指定することでグラフの見た目を変更できる.
ここでは例として,引数 s と alpha を用いて,各マーカの大きさと透明度を指定している.
plt.scatter(df['最高気温'], df['客数'], s=100, alpha=0.5)
plt.title('最高気温と客数の関係')
plt.xlabel('最高気温(度)')
plt.ylabel('客数(人)');
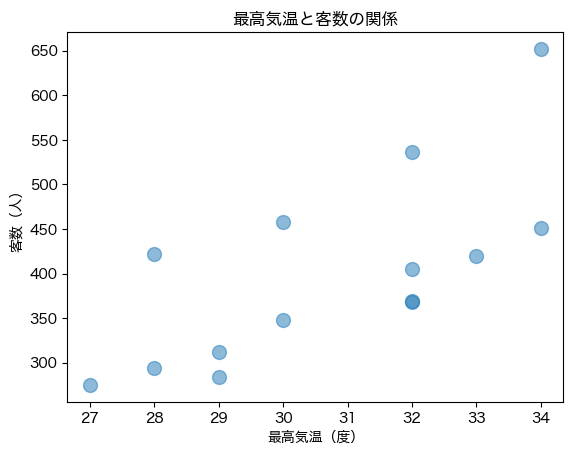
このグラフをみると,最高気温と客数の間には,右肩上がりの関係があるように見える. つまり,最高気温が高くなればなるほど,客数は多くなるような関係がありそうだ.
この関係については,後ほど詳しく考えてみるとして,その前に他のグラフをいくつか紹介する.
棒グラフ#
棒グラフは日常でもよく目にするグラフの一つであり,横軸に項目,縦軸にデータ値をとり,棒の高さでデータの大きさを表している.
Matplotlibでは,pyplot モジュールの bar 関数を用いて棒グラフを描画できる.
plt.bar(X, Y)
先ほどは線グラフで「日付」ごとの「客数」を可視化したが,同じものを棒グラフで表現してみよう.
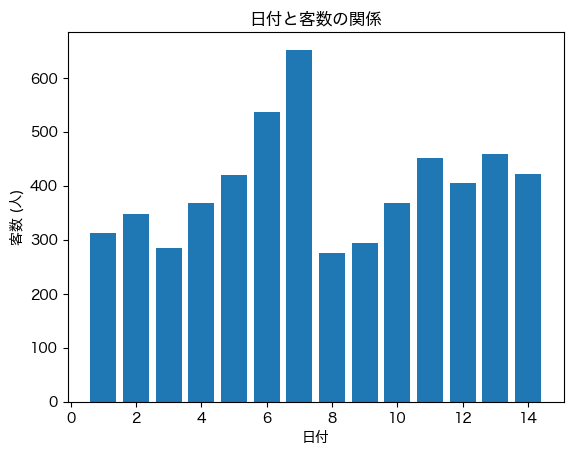
plt.bar(df['日付'], df['客数'])
plt.title('日付と客数の関係') # タイトルを追加
plt.xlabel('日付') # x軸のラベルを追加
plt.ylabel('客数 (人)'); # y軸のラベルを追加
線グラフと棒グラフの使い分け
上記の通り,今回は「日付」と「客数」の関係を,線グラフと棒グラフという2種類の方法で可視化した. グラフより,どちらも同じような情報を表しているが,どんな時に使い分ければよいだろうか?
線グラフの場合は,データ点同士が線で結ばれているため,より日付に応じた変化が強調されているような印象である. 一方,棒グラフの場合は,ある日付と別の日付との間の値の差がより分かりやすい印象である. つまり,線グラフは「変化」が強調されており,棒グラフは「大小の違い」が強調されているわけである.
このことから,横軸の値が連続したデータ(例:年度ごとの売り上げの推移)に関しては,線グラフの方が分かりやすい場面が多い. 一方,横軸の値が独立しているデータ(例:広島,岡山,島根の3地域の売り上げ)については,棒グラフの方が適切だろう.
今回の「日付」と「客数」の場合,横軸は連続した「日付」なので,線グラフの方が適切と思われる.
ただし,「絶対にどちらかを使うべし」という厳密なルールは存在しない. むしろ,そのグラフから自分がどのような主張を行いたいか,に応じて適切なグラフを使い分けることが大切である.
【発展】ヒストグラム#
ヒストグラムは,データを階級で分割し,横軸に階級,縦軸に各階級の度数をとった統計グラフである. 簡単にいうと,データをいくつかの均等な区間に分割するとともに,各区間に含まれるデータの個数を計算し,可視化したものである. 主に,データの分布を調べるために用いられる.
Matplotlibでは,pyplot モジュールの hist 関数を用いてヒストグラムを描画できる.
plt.hist(data)
本来,ヒストグラムはデータ量がある程度多くないと描画が難しいが,今回はひとまず「客数」のデータのヒストグラムを表示してみよう.
plt.hist(df['客数'])
plt.title('客数のヒストグラム')
plt.xlabel('客数')
plt.ylabel('度数');
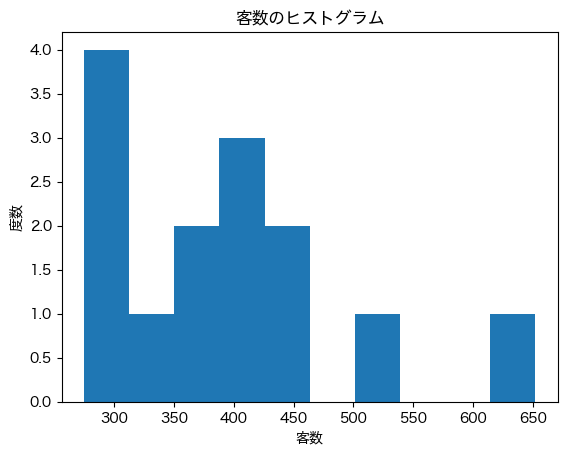
このグラフより,客数は300人から450人くらいの範囲に主に分布しており,客数が500人を超えることは稀であることがわかる.
なお,hist 関数ではデフォルトの分割数として 10 が設定されているが,ここを手動で設定したい場合は引数 bins に分割数を指定すれば良い.
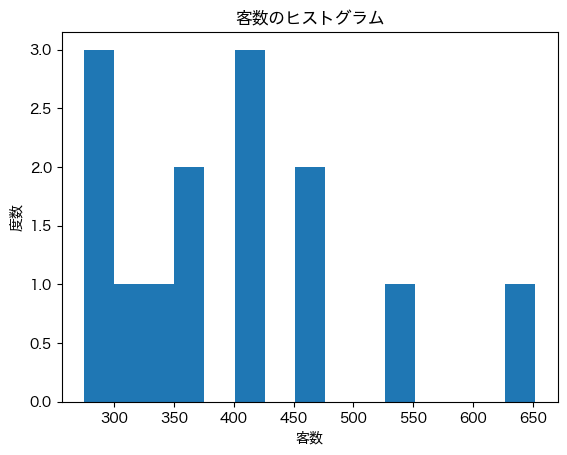
例えば分割数により大きな 15 を設定すると,ヒストグラムの各棒が細くなり,分布の表現がより細かくなる.
plt.hist(df['客数'], bins=15)
plt.title('客数のヒストグラム')
plt.xlabel('客数')
plt.ylabel('度数');
複数のグラフの重ね合わせ#
Matplotlibでは,グラフ作成用関数を繰り返し実行することで,各グラフを重ねて表示することが可能である.
例として,df のデータを第1週目(日付1〜7)と第2週目(日付8〜14)に分け,それぞれ対応する曜日と「客数」の線グラフを重ねて描画してみる.
ここで,日付は月曜始まりとして扱う.つまり,日付1と8は月曜,日付2と9は火曜, …, 日付7と14は日曜となる.
df_1st_week = df[df['日付'] <= 7] # 第1週目のDataFrameを抽出
df_2nd_week = df[df['日付'] > 7] # 第2週目のDataFrameを抽出
days = ['月', '火', '水', '木', '金', '土', '日'] # 横軸となる曜日のリストを作っておく
plt.plot(days, df_1st_week['客数']) # 第1週目の線グラフ作成
plt.plot(days, df_2nd_week['客数']) # 第2週目の線グラフ作成
plt.title('曜日ごとの客数')
plt.xlabel('曜日')
plt.ylabel('客数(人)');
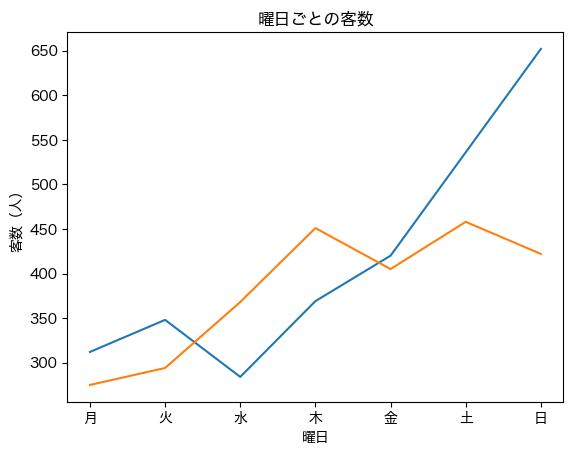
上記からわかるように,線グラフを重ねたい場合は同じセル内で単純に plt.plot を複数実行すればよいことがわかる.
また,各グラフは自動で色分けされている(もちろん,引数で任意の色を指定することもできる).
ただし,上記のグラフだけだと青色と橙色のどちらが1週目と2週目なのか判断がつかない.そのような場合は凡例を表示する必要がある.
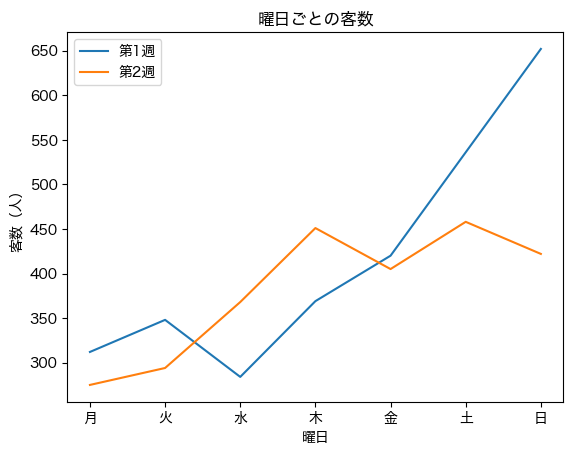
plot 関数の label 引数にグラフの各線の凡例として表示したい文字列を指定した上で,legend 関数を呼び出すことで,グラフ中に凡例を表示することができる.
plt.plot(days, df_1st_week['客数'], label='第1週') # 第1週目の線グラフ作成
plt.plot(days, df_2nd_week['客数'], label='第2週') # 第2週目の線グラフ作成
plt.title('曜日ごとの客数')
plt.xlabel('曜日')
plt.ylabel('客数(人)')
plt.legend();
グラフから読み取れる相関関係#
さて,話を少し戻そう. 散布図の説明をした際に,「最高気温」と「客数」の間に,右肩上がりの関係が確認された.
このように,「x軸の値が大きくなるほど,y軸の値も大きくなる」ような関係性を,正の相関 という. 相関とは,「互いに関係がある」という意味である.
逆に,「x軸の値が大きくなるほど,y軸の値は小さくなる」ことを 負の相関 という. この場合,散布図は右肩下がりになるはずである.
「x軸の値とy軸の値の間に明確な関係がない」場合,無相関 と呼ばれる. この場合,散布図に傾きはみられない.
このような2つの値の相関関係の強さを表す指標として, 相関係数 というものがある. 相関係数は-1から1の値をとり,絶対値が大きいほど関係性が強いことを意味する. 相関係数にはいくつかの定義がありますが,最も代表的なピアソンの積率相関係数 \(r\) は以下の式で計算される.
相関係数の目安
相関係数の値と相関の強さに関して,よく使われる目安は以下の通りである.
相関係数の絶対値 |
目安 |
|---|---|
0.7〜1.0 |
強い相関 |
0.4〜0.7 |
中程度の相関 |
0.2〜0.4 |
弱い相関 |
0.0〜0.2 |
ほとんど相関がない |
ただしこれは絶対的な基準ではないことに注意されたい.
相関係数も要約統計量と同様に,Pandasの機能を用いて計算することができる.
相関係数を計算したい列を含むデータフレームに対し,
DataFrame.corr()
とすれば計算結果が返ってくる. 「最高気温」と「客数」の間の相関係数を計算してみよう.
df[['最高気温', '客数']].corr()
| 最高気温 | 客数 | |
|---|---|---|
| 最高気温 | 1.000000 | 0.697871 |
| 客数 | 0.697871 | 1.000000 |
ここで返されるのは相関行列というものである.この行列の対角成分は同じ変数間の相関係数なので,「1」となる. 「最高気温」と「客数」の間の相関係数を確認するためには,非対角成分の部分に着目すれば良い.
これより,「最高気温」と「客数」の間の相関係数は約0.698であることがわかった. さきほどの目安と照らし合わせると,中程度〜強い正の相関関係があるといえる.
注意
上記の相関行列において,非対角成分は2つあるが,どちらを見ればよいだろうか. 正解は,「どちらでも良い」である.
「最高気温」と「客数」の間の相関も,その逆である「客数」と「最高気温」の間の相関も,同じ意味を持つ. これは,上述の相関係数において \(x\) と \(y\) を入れ替えても本質的な計算は変わらないことからも明らかである. つまり,相関行列は相関行列は対称行列の一種である.
このように,データから平均値など要約統計量を計算したり,散布図などを描画して可視化してみたり,相関係数を計算したりすることで,データの中の性質や関係性を理解したり分析したりすることができる. 今回紹介したPandasやMatplotlibのように,Pythonにはこのようなデータ分析を実現するための様々なモジュール・ライブラリが揃っているため,それらを駆使することで幅広い応用に展開可能である.
【補足】相関関係と因果関係
相関係数は,あくまで2つの変数の間の関係性の強さを示す指標に過ぎない 今回の分析で「最高気温」と「客数」の間に正の相関があることは分かった. これは,「最高気温が高いとき,アイスクリーム屋の客数も多い」ことを意味している.
しかし,この結果から「最高気温が高いことが 原因 で,結果 としてアイスクリーム屋の客数が増えた」と結論付けることはできないことに注意すること(なぜなら,もしかしたら他にも関係する変数が存在するかもしれないからである). 因果関係があるかどうかを示すためには,より複雑な別の分析を行う必要がある.
Matplotlibによるデータの可視化のまとめ
データを様々な方法で視覚的わかりやすく提示することを可視化と呼ぶ
Matplotlibは,Pythonでよく用いられるグラフ描画ライブラリである
線グラフや棒グラフ,ヒストグラムなど,さまざまなグラフを描画できる

